
[prev] [Table of Contents] [next]
Chapter Eleven - Major / Minor relationships
Minor Scales are compared to major scales in one of two ways:
1) Relative relationship
2) Parallel relationship
Every Major key shares its key signature with a Minor key (of a different letter name). That minor key is known as the Relative Minor of the Major key. (A minor is the relative minor of C major).

The reverse relationship is also true.
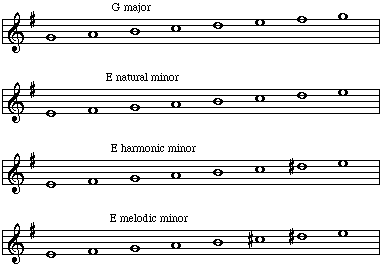
Every Minor key shares its key signature with a Major key (of a different letter name). That Major key is known as the Relative Major of the the Minor key. In the above example, C major is the relative major of A minor. In the following example, G major is the relative major of E minor.

The letter name of a Major key's relative minor is always the same letter name as the 6th scale degree of that same major scale.
example: The sixth note of F major is "D", hence D minor is the relative minor of the F major.

Conversely, the letter name of a minor key's relative major is the same letter name as the 3rd scale degree of that minor scale
example: The third note of D minor is "F", therefore F major is the relative major of D minor.
The relative minor is in the natural minor form. If the harmonic or melodic forms are needed one must make the following changes to the natural minor scale:
Harmonic minor = natural minor with a raised 7th scale degree.
(all other tones unchanged)
Melodic minor = natural minor with a raised 6th and 7th scale degree.
(all other tones unchanged)
R = Raise One Half step
| Natural minor | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Harmonic minor | 1 | 2 | 3 | 4 | 5 | 6 | R7 | 8 |
| Melodic minor | 1 | 2 | 3 | 4 | 5 | R6 | R7 | 8 |
Example
| Scale Degree | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| G Major Scale | G | A | B | C | D | E | F# | G |
| Relative minor begins on the sixth note of major | ||||||||
| E Natural minor | E | F# | G | A | B | C | D | E |
| E Harmonic minor | E | F# | G | A | B | C | D# | E |
| E Melodic minor | E | F# | G | A | B | C# | D# | E |
Circle of Fifths
The circle of fifths shown in the chapter on major key signatures can be used with the corresponding relative minor keys.
The parallel minor of any major key is the minor key that has the same letter name. (C minor is the parallel minor of C major.)

The reverse relationship is also true.
The parallel major of any minor key is the major key that has the same letter name. (D major is the parallel major of D minor.)

When comparing the major and minor forms in their parallel relationship it is customary to use the major scale as the standard model. The minor forms are defined as having alterations to the major form.
L = Lower One Half Step
| Major scale | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Natural minor | 1 | 2 | L3* | 4 | 5 | L6 | L7 | 8 |
| Harmonic minor | 1 | 2 | L3 | 4 | 5 | L6 | 7 | 8 |
| Melodic minor | 1 | 2 | L3 | 4 | 5 | 6 | 7 | 8 |
* The lowered notes are sometimes referred to as "Flatted" i.e. "b3", however in the Sharp keys (G, D, A, E, B F# C#) some of the lowered notes are not "flats" but instead are "naturals". (see example 2)
| Scale Degree | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| C Major Scale | C | D | E | F | G | A | B | C |
| Parallel minor begins on the same note as major | ||||||||
| C Natural minor | C | D | Eb | F | G | Ab | Bb | C |
| C Harmonic minor | C | D | Eb | F | G | Ab | B | C |
| C Melodic minor | C | D | Eb | F | G | A | B | C |

| Scale Degree | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| A Major Scale | A | B | C# | D | E | F# | G# | A |
| Parallel minor begins on the same note as major | ||||||||
| A Natural minor | A | B | C | D | E | F | G | A |
| A Harmonic minor | A | B | C | D | E | F | G# | A |
| A Melodic minor | A | B | C | D | E | F# | G# | A |

Notice that the melodic minor form has all of the same notes as the parallel major except the third scale degree. It is the third scale degree that most clearly distinguishes a scale as major or minor. As you change from the natural minor form to the harmonic and melodic forms, you are moving back towards the parallel major scale
Although it is not as common,the Natural minor scale could be used as the standard from which comparisons are made.
R = Raise One Half step
| Natural minor | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Harmonic minor | 1 | 2 | 3 | 4 | 5 | 6 | R7 | 8 |
| Melodic minor | 1 | 2 | 3 | 4 | 5 | R6 | R7 | 8 |
| Major scale | 1 | 2 | R3 | 4 | 5 | R6 | R7 | 8 |
Example
| C Natural minor | C | D | Eb | F | G | Ab | Bb | C |
| C Harmonic minor | C | D | Eb | F | G | Ab | B | C |
| C Melodic minor | C | D | Eb | F | G | A | B | C |
| C Major scale | C | D | E | F | G | A | B | C |

This example again illustrates how the changes made to the natural minor form (to create the harmonic and melodic forms) are changes that move towards the notes of the parallel major scale
Another example in the key of A:
| A Natural minor | A | B | C | D | E | F | G | A |
| A Harmonic minor | A | B | C | D | E | F | G# | A |
| A Melodic minor | A | B | C | D | E | F# | G# | A |
| A Major scale | A | B | C# | D | E | F# | G# | A |

[prev] [Table of Contents] [next]